Online Certificate

 

Google Classroom

 Google Classroom

Class code: cb263pk

Manipulation

1. Key concepts 

Building 

2. Possibility requirement of the shapes 

• Two trapezoid 
• Six squares 
• 4 rectangles

3. Utility of the shapes 

• Trapezoid is used for building the roofs of house 
• Constructing tables 
• Constructing chairs 

4. Result / output

1.Key Concept: Tree

2.Possibility requirement of the shape 

•    16 triangles 
•     2 squares 

3.Utility of the shapes 

•    Triangles : To makes roofs 

                     While constructing bridges 

•     Squares: To make grids 

                    To make tiles

                    It is used in almost every design as a base or a frame to give it a sense of  

                    stability.

                  

4. Result / output 

                     

Lesson Plan using Coogle.it

Lesson Plan in coggle.it

Construction of Angles

 Using a protractor in manipulative, construct following angles: 

1. Right angle triangle - 90°

   
   

 

2. Obtuse angle - 110°

   

3. Straight angles - 180°

4. Acute angle - 60°

5. Reflex angles ( between 180-360°)

Situating Tool

Rhombus 

Concept Skills

Rhombus is a geometric shape that falls under the category of quadrilaterals. It is a parallelogram with four sides of equal length. The defining characteristic of a rhombus is that all its sides are congruent, meaning they have the same length.

Key concepts related to a rhombus include:

Sides: A rhombus has four sides, and each side is of equal length. The sides are parallel to each other in pairs.

Angles: The opposite angles of a rhombus are equal. Since a rhombus is a parallelogram, its opposite angles are congruent.

Diagonals: The diagonals of a rhombus bisect each other at right angles. This means that the point where the diagonals intersect divides each diagonal into two equal segments.

Symmetry: A rhombus has two lines of symmetry, passing through the intersection of its diagonals. This means that if you fold the rhombus along either of its lines of symmetry, the two halves will perfectly coincide.

Properties shared with parallelograms: A rhombus shares some properties with parallelograms. These include opposite sides being parallel, opposite angles being congruent, consecutive angles being supplementary (adding up to 180 degrees), and consecutive sides being congruent.

Relationship to other shapes: A rhombus is a special type of parallelogram, meaning it possesses all the properties of a parallelogram. It is also a special case of a kite, another quadrilateral with two pairs of adjacent congruent sides.

Process Skills 

Step 1: I used the line segment and created a diagonal line with point A and point B.

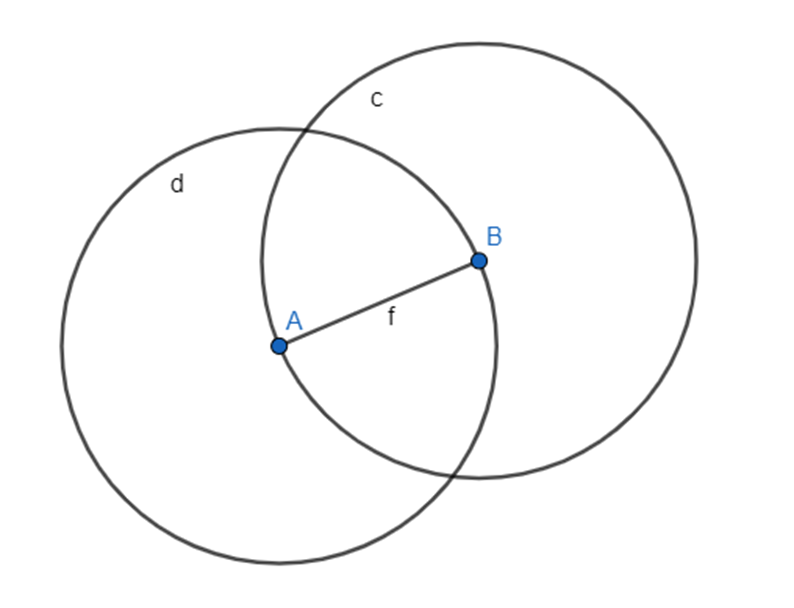
Step 2: I used compass, clicked point A and B to make a circle where point B was at the center.

Step 3: Again I used compass, clicked point B and point C to make a circle where point A is a the center.

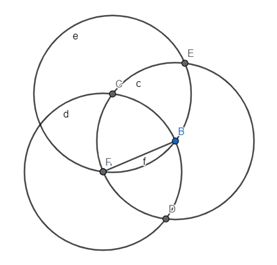
Step 4: Then I used intersect to find the point C.

Step 5: To find the point E I used compass, clicked point A and point C and made a circle. Then using the intersect, I marked point E.

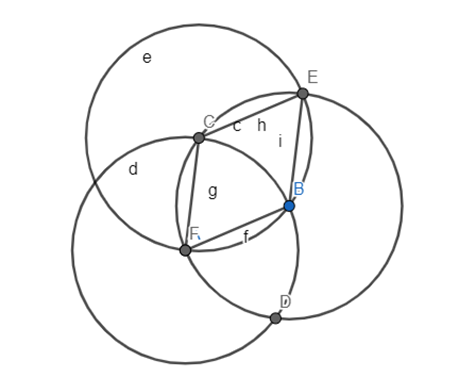
Step 6: Next, I used line segment to join point A, B,C and E.

Step 7: Lastly, using the polygon, I completed the shape rhombus. 

Product skills 

Positive Utilities (Values) and Real-World Applications of Learning about Rhombus:

• Geometry Understanding: Learning about the properties and construction of a rhombus enhances geometric understanding and spatial reasoning skills.
• Problem Solving: Understanding rhombus properties helps develop problem-solving skills by applying geometric concepts to real-world situations, such as calculating areas and perimeters of rhombus-shaped objects or designing structures with rhombus components.
• Art and Design: Rhombus shapes are commonly used in art, architecture, and design. Understanding the properties of a rhombus allows for the creation of aesthetically pleasing patterns and structures.
• Engineering and Construction: Knowledge of rhombus properties can be applied in engineering and construction projects, where rhombus-shaped structures or components are used, such as diamond-shaped windows, roof trusses, or diamond-shaped supports.
• Jewelry and Crafts: Rhombus shapes are often used in jewelry and crafts. Understanding the properties of a rhombus helps in creating and designing unique and visually appealing pieces.
• Mathematical Applications: The study of rhombus is connected to various mathematical concepts, such as symmetry, trigonometry, and coordinate geometry. Understanding rhombus properties can facilitate learning in these areas and their applications in real-world problem solving.

By exploring and applying the concept, process, and product skills related to rhombus construction in GeoGebra, learners can develop a deeper understanding of geometry and its practical applications in the real world.

Balanced Diet